Leetcode1060 Missing Element In Sorted Array

Leecode 1060 Missing Element in Sorted Array

Description

Given a sorted array A of unique numbers, find the K-th missing number starting from the leftmost number of the array.

Example 1: Input: A = [4,7,9,10], K = 1 Output: 5 Explanation: The first missing number is 5.

Example 2: Input: A = [4,7,9,10], K = 3 Output: 8 Explanation: The missing numbers are [5,6,8,…], hence the third missing number is 8. Example 3:

Input: A = [1,2,4], K = 3 Output: 6 Explanation: The missing numbers are [3,5,6,7,…], hence the third missing number is 6.

Note: 1 <= A.length <= 50000 1 <= A[i] <= 1e7 1 <= K <= 1e8

Solution

Use binary search. This question belongs to the third kind of binary search, we need find a condition to eliminate half of the data. Lets see one example:

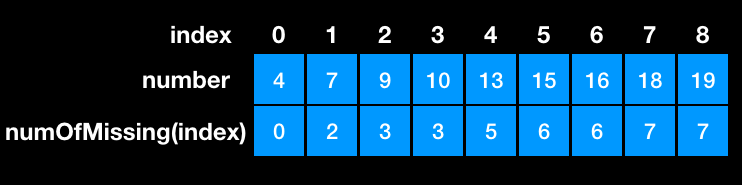
If K = 3, we will stop at number 9. if K = 4, we will stop at number 13.

So the question becomes that we want find the index of the leftmost lower-bound of K. Then the number of missing at index - 1 must less then K. Then we can use nums[index-1] + K - numOfMissing(index-1).

Code

class Solution {
public:
    int missingElement(vector<int>& nums, int k) {
        // assume nums is not empty
        int left = 0;
        int right = nums.size()-1;
        int count = missingCount(nums, right);
        
        if(k > count) {
            return nums[right] + k - count;
        }
        
        while(left < right) {                     /*❶*/
            int mid = left + (right - left) /2 ;
            count = missingCount(nums, mid);
            if(count >= k){
                right = mid;                      /*❷*/
            } else {
                left = mid + 1;
            }
        }
        return nums[left-1] + k - missingCount(nums, left-1);
    }
    
    int missingCount(vector<int>& nums, int idx){
        return nums[idx] - nums[0] - idx;
    }
};

❶ position left will be the lower bound of K. Why?
❷ why right = mid?

Insight💡

Is this the template to find a lower bound of the target?
Is there any other way to solve this problem?
What the time complexity of binary search approach? [O(logn)]